Light Reflection and Refraction: This chapter introduces the fundamental concepts of light and how it behaves when it encounters surfaces. It focuses on two key phenomena: reflection and refraction of light.
*Reflection of Light
Mirror formula and magnification
Laws of reflection
Types of reflection: regular and diffused
Formation of images by spherical mirrors (concave and convex)
Ray diagrams for mirrors
*Refraction of Light
Lens formula and magnification
Laws of refraction
Concept of refractive index
Refraction through glass slab
Refraction by spherical lenses (convex and concave)
Image Formation by Curved Mirrors
1. Concave Mirror (inward curved)
Converging mirror – reflects light rays to a point.
Image formation depends on the object’s distance from the mirror.
| Object Position | Image Position | Image Nature |
|---|---|---|
| At infinity | At focus (F) | Real, inverted, highly diminished |
| Beyond centre (C) | Between F and C | Real, inverted, diminished |
| At centre (C) | At centre (C) | Real, inverted, same size |
| Between F and C | Beyond centre (C) | Real, inverted, enlarged |
| At focus (F) | At infinity | Real, inverted, highly enlarged |
| Between pole (P) and F | Behind the mirror | Virtual, erect, enlarged |
2. Convex Mirror (outward curved)
Diverging mirror – reflects light rays outward.
Always forms virtual, erect, and smaller images behind the mirror, regardless of object position.
Image Formation by Lenses
1. Convex Lens (thicker in the middle)
Converging lens – bends light rays to meet at a point.
| Object Position | Image Position | Image Nature |
|---|---|---|
| At infinity | At focus (F2) | Real, inverted, point-sized |
| Beyond 2F1 | Between F2 and 2F2 | Real, inverted, diminished |
| At 2F1 | At 2F2 | Real, inverted, same size |
| Between F1 and 2F1 | Beyond 2F2 | Real, inverted, enlarged |
| At focus (F1) | At infinity | Real, inverted, highly enlarged |
| Between F1 and lens | Same side as object | Virtual, erect, enlarged |
2. Concave Lens (thinner in the middle)
Diverging lens – spreads light rays outward.
Always forms virtual, erect, and smaller images on the same side as the object.
Ch-1 Chemical Reactions and Equations & Ch-5 Life Processes Question Answers
Chapter- 10 Light Reflection and Refraction Most Important Questions and Answers
1. A 3 cm tall object is placed 18 cm in front of a concave mirror of focal length 12 cm. At what distance from the mirror should a screen be placed to see a sharp image of the object on the screen. Also calculate the height of the image formed.
Answer:
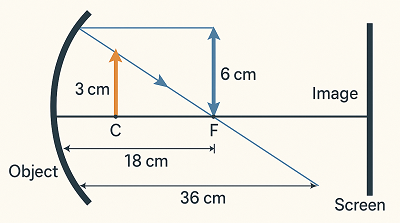
Object in front of concave mirror
Screen should be placed 36 cm in front of mirror.
Height of image = 6 cm (real, inverted).
Given:
$$h_o = 3 \text{ cm}, u = -18 \text{ cm}, f = -12 \text{ cm}$$
Mirror formula:
$$\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$$
$$\Rightarrow \frac{1}{-12} = \frac{1}{v} + \frac{1}{-18} \Rightarrow \frac{1}{v} = \frac{1}{-12} + \frac{1}{18} = -\frac{1}{36}$$
$$\Rightarrow v = -36 \text{ cm}$$
Magnification:
$$m = \frac{v}{u} = \frac{-36}{-18} = 2$$
$$h_i = m \times h_o = 2 \times 3 = 6 \text{ cm}$$
2. An object is placed at a distance of 10 cm from a convex mirror of focal length 5 cm.
(i) Draw a ray diagram showing the formation of image.
(ii) State two characteristics of the image formed.
(iii) Calculate the distance of the image from mirror.
Answer: Convex mirror image
(i) Ray diagram (to be drawn separately).
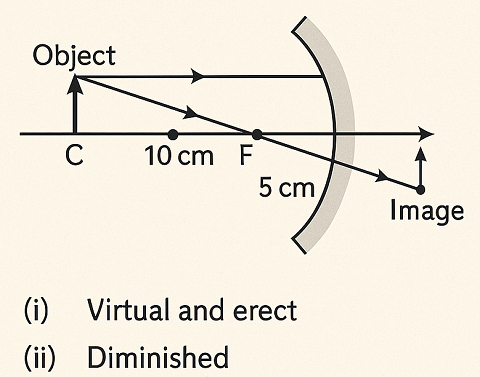
(ii) Virtual, erect, and diminished.
(iii) Image distance = 3.33 cm behind the mirror.
Given:
$$u = -10 \text{ cm}, f = +5 \text{ cm}$$
$$\frac{1}{v} = \frac{1}{f} – \frac{1}{u} = \frac{1}{5} + \frac{1}{10} = \frac{3}{10} \Rightarrow v = 3.33 \text{ cm}$$
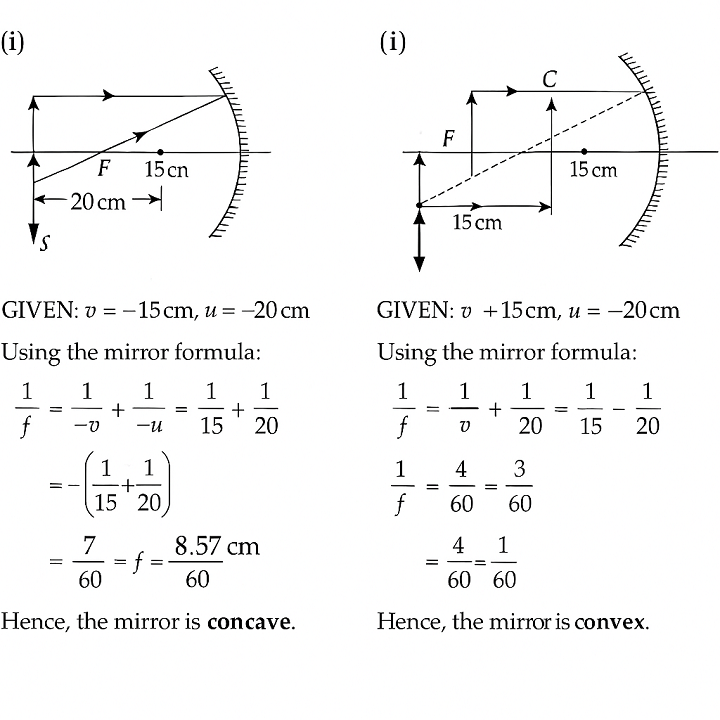
3. An object placed 20 cm in front of a mirror is found to form an image at 15 cm
(i) in front of it,
(ii) behind the mirror.
Find the focal length of the mirror and the kind of mirror in each case.
Answer:
4. An object is placed at a distance of 10 cm from a concave mirror of focal length 20 cm.
(i) Draw a ray diagram for the formation of image.
(ii) Calculate the image distance.
(iii) State two characteristics of the image formed.
Answer:
Given:
Object distance, $$u = -10 \, \text{cm}$$ (object is in front of the mirror, so it’s negative)
Focal length, $$f = -20 \, \text{cm}$$ (for concave mirror, focal length is negative)
(i) Ray Diagram
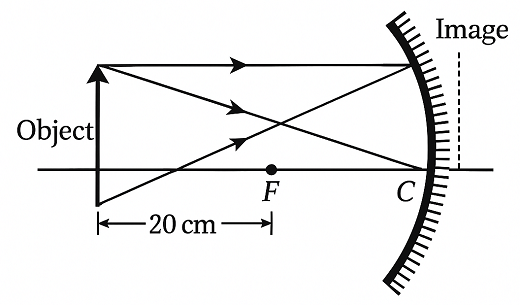
(ii) Image Distance Calculation
Use mirror formula: $$\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$$
Substitute values: $$\frac{1}{-20} = \frac{1}{v} + \frac{1}{-10} \Rightarrow \frac{1}{v} = \frac{1}{-20} + \frac{1}{10} \Rightarrow \frac{1}{v} = \frac{-1 + 2}{20} = \frac{1}{20}$$
$$\therefore v = 20 \, \text{cm}$$
(iii) Two Characteristics of the Image
Magnified – the image is larger than the object.
Virtual and Erect – because the object is placed between the pole and focus of a concave mirror.
5. If an object 10 cm high is placed at a distance of 36 cm from a concave mirror of focal length 12 cm, find the position, nature and height of the image.
Answer:
Given:
Object height, ho=10 cm
Object distance, u=−36 cm
Focal length, f=−12 cm (concave mirror)
(i) Image Position (v)
Using the mirror formula: $$\frac{1}{f} = \frac{1}{v} + \frac{1}{u}$$
Substitute values: $$\frac{1}{-12} = \frac{1}{v} + \frac{1}{-36} \Rightarrow \frac{1}{v} = \frac{1}{-12} + \frac{1}{36} = \frac{-3 + 1}{36} = \frac{-2}{36} = \frac{-1}{18}$$
$$\Rightarrow v = -18 \, \text{cm}$$
Image is formed 18 cm in front of the mirror.
(ii) Magnification (m)
$$m = \frac{h_i}{h_o} = \frac{-v}{u} = \frac{-(-18)}{-36} = \frac{18}{-36} = -0.5$$
$$h_i = m \times h_o = -0.5 \times 10 = -5 \, \text{cm}$$
(iii) Conclusion
Height: 5 cm, inverted
Position: 18 cm in front of the mirror
Nature: Real and Inverted (since image distance is negative and height is negative)
6. If the magnification of an object of size 1 m is 2, what is the size of the image?
Answer:
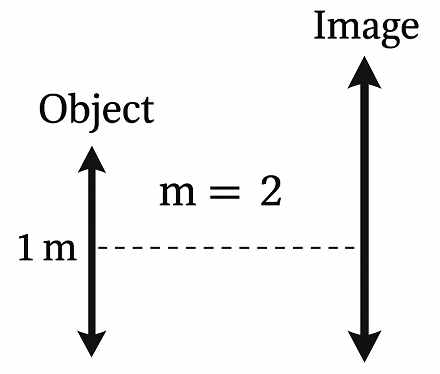
Given
Object size (height), ho=1 m
Magnification, m=2
Formula:
$$m = \frac{h_i}{h_o} \Rightarrow h_i = m \times h_o$$
Substitute the values: $$h_i = 2 \times 1 = 2 \, \text{m}$$
The size of the image is 2 meters.
7. In an experiment with a rectangular glass slab, a student observed that a ray of light incident at an angle of 60° with the normal on one face of the slab, after refraction, strikes the opposite face of the slab before emerging out in air making an angle of 42° with the normal. Draw a labelled ray diagram to show the path of this ray. What value would you assign to the angle of refraction and angle of emergence?
Answer:

In the given experiment:
- A ray of light is incident at 60° with the normal on one face of a rectangular glass slab.
- It undergoes refraction inside the glass slab.
- It emerges from the opposite face, making an angle of 42° with the normal.
However, in normal conditions for a rectangular glass slab, the angle of incidence and angle of emergence are equal, while the angle of refraction inside the glass slab is smaller due to the denser medium (glass).
But since here it’s given that the incident angle is 60° and the emergent angle is 42°, it means the emergent ray bends less than expected—a rare situation unless specified with different conditions.
Assuming it’s a simple refraction setup, the usual interpretation is:
Angle of incidence i = 60°
Angle of refraction r = 42° (inside the slab)
Angle of emergence e = 60° (emerges back into air, hence equals incidence)



